With the number of hours you spend in front of a computer, has it ever crossed your mind to wonder whether the computer has a language too? And that this language uses binary numbers?
Maybe you know about your computer’s special coding language?
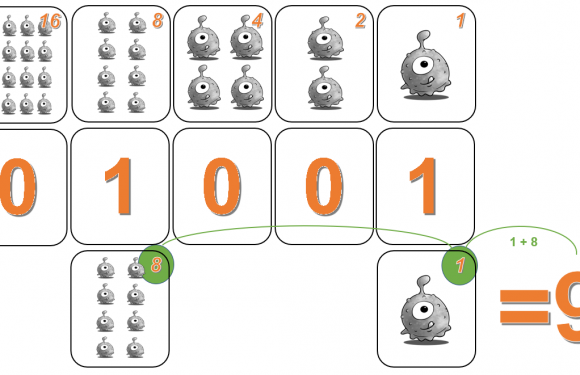
So, computers and other digital electronics make use of a language known as binary code. Binary (based on binary numbers or base-2) is a numeral system that uses just 0s and 1s to represent all data used by a computer. When binary numbers are grouped together they are called bytes.
What makes the binary numbers important?
With binary, it became possible to have exact states which would not have small errors. Way back in history, computers made use of something called analog in order to solve problems. But this wasn’t as accurate as binary code and so those computers were largely replaced by the digital computer which used binary code. The analog method of using continuously changing attributes – such as electrical, mechanical or hydraulic qualities – could cause small errors which, when iterated, could cause complex issues. But with binary numbers, these errors are avoided and the chance of committing errors is much, much smaller.
Binary numbers simplify the design of computers and related technologies. Computers need many transistors to accomplish what they have to accomplish, but through binary numbers, it became easier and less expensive. It needs the least amount of necessary circuitry, which results in the least amount of space, energy consumption, and cost. It also provides safety for reliability.
The use of binary numbers increased the expressive power of the binary circuits that cut down the cost of a computer and made a more powerful computer for the same amount of money. Also, the use of binary numbers maximises the expressive power of binary circuits.
But why binary?
Computers use binary because they can only read and store an on or off charge. Zero (0) is equivalent to off and one (1) is equivalent to on. It is extremely robust in transmission because any noise tends to be neither fully “on” or “off” and is easy to reject. Any system that has an “on” and “off” or a “high” and “low” state can be used to encode and/or manipulate data.
The logic of binary is easy to understand and has the capacity to build any type of logic gates.
The computer system executes many processes that seem complex, but they’re not all that complex when they’re broken down. Just like with binary; it looks complicated, but when you have familiarised your self with it, it will just be a piece of cake.
Why not try some of our Activities for binary numbers and have some fun learning!